A Teremtés geometriája
Reveláció
Ebben az írásban röviden és
érthetően bemutatom, hogy a rendelkezésre álló kozmológiai mérések milyen geometriában
értelmezhetők, vagyis a táguló Világegyetemünk valójában milyen geometriát
alkot.
Ezen mérések szerint a Világegyetem
egyre tágul, a tágulás mértéke gyorsul, sebessége pedig arányos az objektumok
egymástól való távolságával. Képszerűen ma ezt egy táguló tölcsér formájában
ábrázolják:
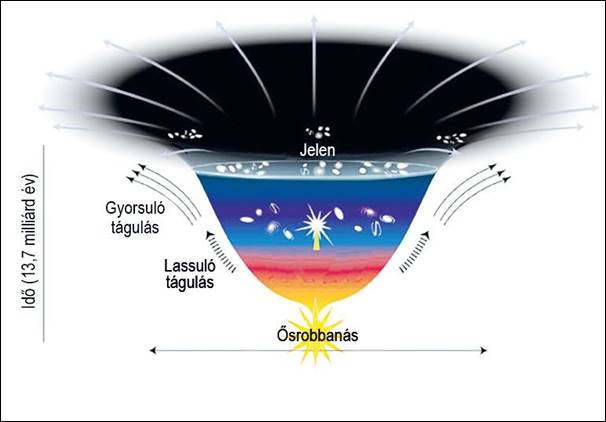
(Forrás: https://termvil.hu/2020/01/17/ertjuk-e-a-tagulo-univerzumot/).
A függőleges
tengelyen az idő múlása, a vízszintes
tengelyen pedig a térbeli Univerzumunk egy kétdimenziós síkja látható.
Az ábrázolás
tulajdonképpen egy fantáziarajz, amelyen az Univerzumról készült mérési
eredményeket próbálják bemutatni. Az ábrázolásból nem derül ki,
hogy az Univerzumunk miért tágul, és miért gyorsulva tágul. Jelen dolgozatban
viszont erre is választ kapunk, de ehhez először meg kell ismernünk a téridőről
alkotott jelenlegi felfogásunkat.
Téridőről Hermann Minkowski óta
beszélhetünk, addig a fizika a teret és az időt külön mértékegységgel kezelte.
Minkowski német matematikus, korának világhírű, élvonalbeli tudósa volt. Fő
kutatási területe a számok geometriája volt, közérthetőbben fogalmazva:
geometriailag leírta, vagyis láthatóvá tette az addig csak számokkal
megfogalmazott, leírt dolgokat.
Minkowski 1907-ben felismerte, hogy a
relativitáselmélet, amelyet 1905-ben egy korábbi tanítványa, Einstein mutatott
be, és amely Hendrik Lorentz és mások korábbi munkáin alapult, a négydimenziós
térben geometriailag is leírható. Ebben a négydimenziós koordinátarendszerben a
tér és idő egyesül, vagyis az egyébként láthatatlan, fizikailag
érzékelhetetlen idődimenzió láthatóvá válik, geometriailag
megjeleníthető! A német természettudósok és fizikusok 80. találkozóján
1908. szeptember 21-én felismerését ezekkel a szavakkal adta elő: “Bemutatom
Önöknek a tér és idő elméletét, amely a kísérleti fizika táptalajából nőtt
ki és ebben rejlik az ereje. Forradalmian új. Mostantól az önmagában vett
tér és idő arra ítéltetett, hogy elenyésszen a homályban és csupán a kettejük
egyesítése képes arra, hogy megőrizze a független valóságot.” (Kiemelések
tőlem.)
A munkássága korszakalkotó, hiszen gondoljunk
csak bele: a környezetünk valójában egy négydimenziós folyam, de
érzékszerveinkkel ebből csak hármat, a három térdimenziót érzékeljük. A
negyediket közvetlenül nem érzékeljük, tudunk a létezéséről, de csak közvetve,
valamilyen háromdimenzióban történő mozgással (homokóra, toronyóra, kvarcóra,
csillagok, stb.) tudjuk jellemezni, valójában fogalmunk sincs a tulajdonképpeni
természetéről.
Minkowski géniusza abban áll, hogy matematikusként
láthatóvá tette az időmenti tulajdonságokat azon mérések segítségével, melyeket
a fizikusok végeztek, vagyis a fizikusok tér és idő jellegű méréseit egységes
geometriai rendszerbe foglalta.
Sajnálatos módon a fenti bejelentése után
néhány hónapra tragikus hirtelenséggel fiatalon meghal, így nem állt módjában
pontosítani, értelmezni a felismerését. Ezt jó száz év után mi most megtesszük,
és látni fogjuk, hogy e kis korrekció által láthatóvá válik az Univerzumunk
tényleges szerkezete.
1.
Téridő szerkezete a jelenlegi értelmezés
szerint
Többségünk nem
találkozott tanulmányai során ezzel az ismerettel, viszont fontosnak tartom,
hogy ezzel a triviális dologgal minél többen tisztában legyenek, hiszen ez
legalább olyan fontos, és semmivel sem bonyolultabb, mint mondjuk a mechanika,
vagy a termodinamika alapismeretei. Én magam Fercsik János: A
relativitáselmélet szemlélete című kiváló, és közérthetően megfogalmazott
könyvéből értettem meg a téridő szerkezetét, ebből idézem most a legfontosabb
ismereteket: (Aki ismeri az anyagot, átugorhatja a kékkel kiemelt
idézetet.)
"Minkowski négy, egymásra merőleges (!!) tengelyt használ
(»hosszúság«, »szélesség«, »magasság« és »idő« tengelyek), mert a téridő
négydimenziós. Mind a négy tengelyt azonos mértékegységben kell skálázni;
egységesen méterekben történik a mérés és a skálázás. …
Mivel a fény sebessége
légüres térben a tömegektől távol, kerek értékben c = 3x108 m/sec,
így a hagyományosan mért t* (sec) időadatot méterekké … tudjuk átszámítani.
Például fél másodperc … 150 000 kilométer időnek felel meg.
Még egy nehézség van. Jelenlegi szemléletünkkel semmiképpen sem
tudjuk elképzelni a téridő négy, egymásra merőleges tengelyét. Ezért megint úgy
segítünk magunkon, hogy a téridőnek csak két koordinátáját (»dimenzióját«)
ábrázoljuk a rajz síkján: az x(m) és a t(m) (»hosszúság« és »idő«) koordinátákat.
…
A téridő ilyetén ábrázolását látjuk a 4. ábrán. A K
koordinátarendszer x-tengelyére a hosszúságokat (»távolságokat«) skáláztuk 108
m-es léptékben. Ezt a K koordináta-rendszert természetesen egy testhez
rögzítjük, középpontjánál fogva. Egyelőre rögzítsük saját személyünkhöz, és
akkor magunk vagyunk a téridő K koordinátarendszerének O középpontjában
(origójában). Az x-tengelynek mindig ugyanabba az irányba kell mutatnia;
mutasson egyelőre pl. mindig a Sirius csillagra a +x-tengely, az ellenkező
irányba pedig a -x-tengely.
Íme: előttünk áll a téridő, amelyben szerves egységbe forr össze
tér és idő. Ábrázolása egyszerű, szemlélete kézenfekvő. Minkowski ezt nevezte
el »Világ«-nak, a benne nyugvó és mozgó testek pályáit pedig
»világ-vonalak«-nak.

Testek mozgása téridőben
A téridőben, a hozzánk rögzített K koordinátarendszerhez (továbbiakban:
K rendszer) képest nyugalomban lévő test világvonala a t tengellyel párhuzamos
egyenes lesz (5. ábra, I. világvonal). Ez természetes, hiszen a test x
koordinátája nem változik, mivel "helyben marad", csupán
időkoordinátája [t(m)] vesz fel egyre nagyobb és nagyobb értéket az idő
folyamatos múlása miatt. Az 5. ábrán példaként feltüntettük a Siriussal
ellenkező irányban -1,5x108 m távolságban, hozzánk képest
nyugalomban lévő test világvonalát. (I.)
Ha a test a K rendszerben, az x-tengely mentén egyenes vonalú,
egyenletes mozgást végez állandó sebességgel, akkor a világvonala az ábrán egy
ferde egyenes lesz. Ennek oka az, hogy az idő múlása folytán a test t
koordinátája növekszik, eközben az x-koordinátája is folyamatosan egyenletesen
változik, mivel az x-tengelyen futva "helyét változtatja". Az 5.
ábrán példaként berajzoltuk az origóból a Sirius csillag felé küldött v2 = +
1,5x108 [m/sec] sebességű rakéta világvonalát. (II. sz. világvonal.)
Hogyan fest a fénysugár világvonala a tér-időben?
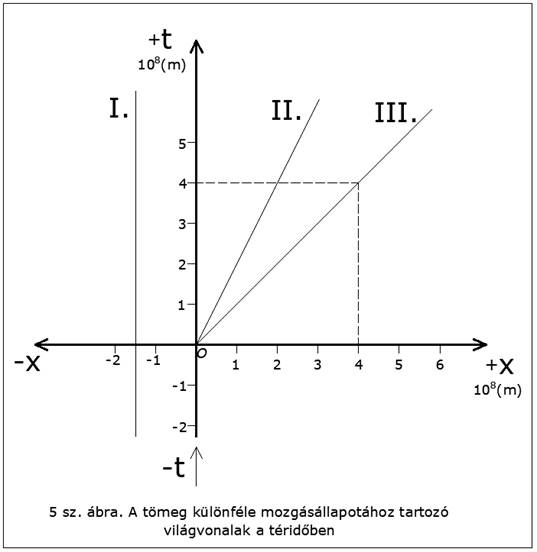
Az A. A. Michelson-R. W. Morley-kísérlet óta tudjuk, hogy a fény
terjedési sebessége légüres térben, nagy tömegektől távol állandó, c= 3x108
(m/sec) érték, és független a vonatkoztatási rendszertől. (A fénysebesség a
létező felső határsebesség, amelyet reális test csak megközelíthet, de el nem
érhet. Fénysebességgel csak az elektromágneses sugárzás, a gravitációs hatás és
a neutrínó haladhat.) Az origóból az x-tengely mentén a Sirius felé küldött
fénysugár világvonalát az 5. ábrán a III. egyenes adja. Az ábrán megjelöltük
azt is, hogy pl. t = +4x108 (m) idő múlva a fénysugár már x = +4x108
(m) távolságra jut el.
Lényeges: valódi testek világvonalai mindig
"meredekebbek" a rajzon a fény világvonalánál, mert a fénysebesség a
létező legnagyobb sebesség. (...)
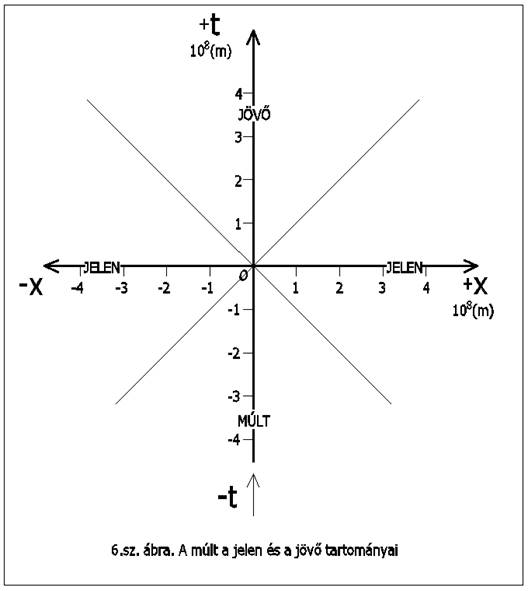
Mivel a K koordinátarendszert saját személyünkhöz rögzítettük
origójánál (O) fogva, az ITT és MOST esemény éppen az origóban van. Számunkra a
t tengely pozitív ága - az idő folyamatos előrehaladása miatt - jelöli ki a
JÖVŐ-t, míg a t tengely negatív ága a múltat mutatja. Úgy észleljük, hogy az
ábrán az x-tengely »felett« a JÖVŐ-beli események fognak megtörténni, az
x-tengely »alatt« a múltbeli események történtek meg, az x-tengelyen pedig a jelenben
zajló események történnek. Ezt a 6. ábrára ráírtuk.
Ki-ki a saját koordinátarendszerében - természetesen a - t
tengelyen - megjelölheti eddigi élete fontosabb dátumait. És ha tudná (a jövőbe
látna), bejelölhetné a + t tengelyre életének ezután bekövetkező jelentősebb
eseményeit. A jelen pillanatot, az ITT és MOST eseményt bárki
koordinátarendszerében az origó (O) mutatja.
A sajátidő
Mindenekelőtt: a téridőben (amikor tehát az egyik koordináta az
idő) nem érvényes a Pitagorasz-tétel. A téridőben levő olyan derékszögű
háromszögnél, amelynek egyik befogója időjellegű, a befogók négyzetének
különbsége egyenlő az átfogó négyzetével. …
A 8. sz. ábrán egy v=+180 000 (km/sec) sebességű rakéta
világvonala látható, amit az x-tengely mentén futva áthalad
koordinátarendszerünk origóján. Az ábra szerint a rakéta éppen ITT ÉS MOST van,
tehát az O origóban látjuk. A mi (K rendszerbeli) méréseink és észleléseink
szerint ez a rakéta ∆t = 5x108 (m) idő eltelte után valóban ∆x
= 3x108 (m) távolságra jut el az x-tengelyünk mentén: bekövetkezik a
B esemény. … (A számítás ∆x = β x ∆t = 0,6 x5 x 108
= 3 x 108 (m) módját később közöljük.)
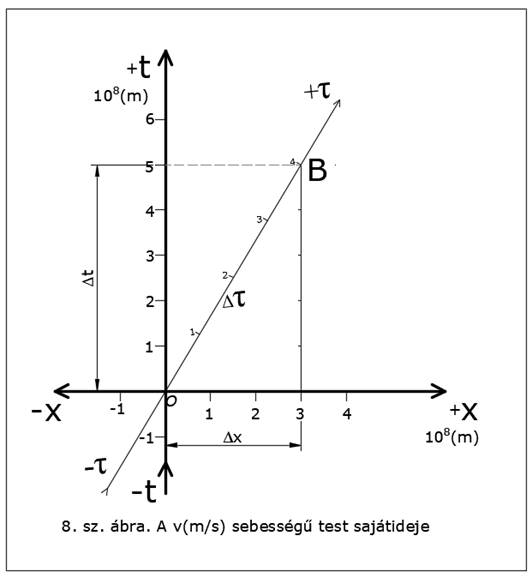
Figyeljük meg: saját K téridő-koordinátarendszerünkben a rakéta
a miáltalunk mért ∆t (m) idő alatt ∆x (m) távolságot tett meg. Ez a
… téridőháromszög két befogója. A téridőháromszög átfogója pedig – mivel az a
rakéta világvonalán van – a rakéta sajátidejét: a rakétában esetleg utazók
számára eltelt ∆τ (m) időtartamot mutatja! Ez a ∆τ (m)
átfogó pedig kisebb, mint a ∆t (m) befogó. Látjuk: a mozgó test számára
lassabban múlik az idő.”
„… amíg a három térkoordinátával dolgozó térgeometria
eukleideszi geometria, (a háromdimenziós tér: eukleidészi tér), addig a
négydimenziós téridő hiperbolikus tulajdonságokkal bír! Úgy mondjuk, a téridő
nem-eukleidészi, hiperbolikus. A speciális relativitáselméletnek ez az egyik
legfontosabb felismerése.”
A
bolygónk valahogy így görbíti meg a teret a www.csillagaszat.hu
internetes oldalon található ábra szerint.
2.
A
jelenlegi értelmezés kritikája
Eddig
az idézet, és most vizsgáljuk meg közösen az állításokat. Először is szögezzük
le, hogy a feltüntetett értékek fizikai mérésekből származnak, tehát ez az
ábrázolás megpróbálja geometriailag leképezni a testek mozgásának vizsgálata
során megfigyelt észleléseket. Ezt hangsúlyozza Minkowski is a bemutató
előadásában, mikor azt mondja, hogy elmélete „a kísérleti fizika táptalajából nőtt ki”.
A
testek mozgásánál az imént ezt olvastuk: „A
téridőben, a hozzánk rögzített K koordinátarendszerhez (továbbiakban: K
rendszer) képest nyugalomban lévő test világvonala a t tengellyel párhuzamos
egyenes lesz (5. ábra, I. világvonal). Ez természetes, hiszen a test x
koordinátája nem változik, mivel "helyben marad", csupán
időkoordinátája [t(m)] vesz fel egyre nagyobb és nagyobb értéket az idő
folyamatos múlása miatt.”
–
Tehát a hozzánk képest nyugalomban lévő test időkoordinátája folyamatosan nő! – Ez egy rendkívül fontos megállapítás, és nézzük meg,
valójában mit is jelent: Az történik, hogy amig mi az O origóban
ácsorgunk, addig a térben hozzánk képest változatlan távolságban lévő test az
idődimenzió mentén másodpercenként 3x108 (m/s) sebességgel távolodik
tőlünk. Nem történhet másként, hiszen mint tudjuk, „az idő nem áll meg”, minden
létező tömeg időkoordinátája folyamatosan nő.
Na
jó, de mi a helyzet a mi időkoordinátánkkal? Az változatlan? Miért? Hiszen
ezzel gyakorlatilag kikerülünk az éterbe, vagyis a mozdulatlan létezésbe. Ezt
az igen fontos körülményt a Minkowski-féle ábrázolás nem fogalmazza meg, és a
következményeit nem is kezeli. A nagy tudósnak nem volt ideje kritikus
szemmel „visszanézni” a művére, és ezt a tudóstársak sem teszik meg. Nem veszik
észre, hogy
a
méréseket végző objektumok időkoordinátája is folyamatosan nő a vizsgált
objektummal együtt!
Minkowski
tekintélye, és a speciális tudása olyan nagy volt, hogy a tudóstársadalom
kritikátlanul elfogadta az elméletét. Végül is a segítségével használható
eredményeket kaptak, igaz, csavarni kellett egyet a Pitagorasz-tételen, de a
tétel fordítva felírva már működött. A gyakorlati számításoknál a modell
használható volt, viszont az elméleti fizikát zsákutcában tartotta mind ez
idáig.
3.
Téridő ábrázolás a korrigált értelmezés
szerint
És
most nézzük meg, hogyan alakul a 8. sz. ábra, ha figyelembe vesszük az O
origó időmenti mozgását. Ekkor azt látjuk, hogy a K rendszer az egész
JELEN-beni környezetével együtt mozog az idődimenzió mentén a múltól a jövő
felé. – Hogyan? Milyen sebességgel? És itt jön a korszakalkotó megállapítás,
hogy tudniillik közel FÉNYSEBESSÉGGEL! Azért csak „közel”, mert mint tudjuk,
fénysebességet reális test el nem érhet, csak az elektromágneses sugárzás.
Minél nagyobb, vagy minél gyorsabban mozog egy test a térben, annál lassúbb ez
az idődimenzió menti sebessége. Ha ennek figyelembevételével szerkesztjük meg a
rakéta világvonalát, akkor mindjárt helyére kerülnek a dolgok: Pl. nem kell az
időt a múlt-jövő irányára szög alatt ábrázolnunk, hanem ábrázolhatjuk
párhuzamosan az időtengellyel, ahogyan az a valóságban is történik. A térrel
ellentétben az idő nem tud görbülni, az idő mindig nyílegyenesen a múltból a
jövő felé mutat.
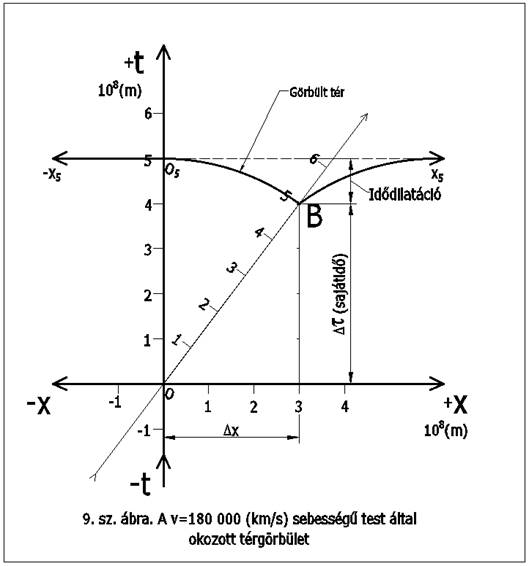
Ha belátjuk és
elfogadjuk, hogy a mérést végző megfigyelő időkoordinátája is folyamatosan nő,
vagyis az X tengely is mozog az idődimenzió mentén, akkor 5x108 m
idő elteltével a 9. ábrán látható térgörbületet tapasztalunk a B pontban lévő
rakéta körül. (A görbületi sugár szimbolikus, csak az ábrázolhatóságot
szolgálja, valószínűbb, hogy csak a súrlódással érintett környezete görbül.)
Viszont az tény, mérések igazolják, hogy a rakéta időmenti mozgása lassul,
kevesebb utat tesz meg az idődimenzió mentén.
A relativitáselmélet
alapján ma úgy mondják, hogy a benne utazók számára lassabban telik az idő. És
itt van a baj, mert ettől a megfogalmazástól lett az idő, illetve téridő
felfoghatatlanul misztikus és elképzelhetetlen. Tudniillik most már látjuk,
hogy nem az idő „múlik”, hanem a JELEN halad, mozog, megy az idődimenzió mentén
a MÚLT-ból a JÖVŐ felé.
Továbbá azt is látjuk,
hogy ha egy tömegpont a térben mozog, akkor annak az idődimenzió menti mozgása
lassul, kevesebbet halad az időben előre a mozdulatlan környezeténél. Ezt
hívják a fizikusok idődilatációnak, illetve a mozgó test kisebb időértékét
sajátidőnek, amit a 9. ábra alapján már a Pitagorasz-tétel eredeti formájával
számolhatunk!
Az időt mindnyájunk
számára a t tengely mutatja, vagyis az időmenti mozgást – köznapian fogalmazva:
az idő múlását – a t tengely mentén mérjük, nem pedig ferdén, ahogyan a 8.
ábrán láttuk, hiszen az már téridő távolságot mutat.
Mérések szerint a
rakétában elhelyezett órán négy másodperc elegendő ahhoz, hogy elérje a B
pontot, pedig a nyugvó rendszerek 5 másodperc múlva fogják elérni azt a –
mondjuk így – időhorizontot, amelyen a B esemény be fog következni. Ez érdekes.
Hogyan lehetséges ez? – Úgy, hogy nem jó a megfogalmazás: Az észlelt fizikai
jelenség megfogalmazása helyesen így hangzik: A térben mozdulatlan objektum az
idődimenzió mentén nagyobb távolságot tesz meg, mint az térben mozgó objektum.
A fizikusok gyakran
téridő görbületről beszélnek, de nekünk tudatosítanunk kell magunkban, hogy
valójában csak térgörbületről van szó, hiszen tudjuk: az idő nem lehet görbe!
Az idő mindig nyílegyenesen a múltból a jövő felé mutat. Ezért mi csak
térgörbületről beszélünk. A görbületet a térbeli mozgás hozza létre: Amelyik
objektum elkezd a térben mozogni, annak csökken az időmenti haladása. Ez
történik a mi rakétánkkal is, az időmenti haladása a mozdulatlan térbeli
környezetéhez képest 1/3 szekundumnyi távolsággal elmarad. Ezt mérések
igazolják. És mivel nem szakad el a tértől, tehát a mozgó test megmarad
ugyanebben a dimenzióban, akkor ez csak úgy következhet be, hogy az egyébként
sík tér meggörbül.
Az ábrából kitűnik, hogy
a tér minden egyes nyugvó pontjának ugyanazon időmenti sebesség áll
rendelkezésére, ami a fénysebesség. Tehát ekkora sebességgel mozog a tér minden
egyes nyugvó (tömeg nélküli) pontja az idődimenzió mentén. Ha a pont térirányú
mozgásnak indul, akkor az időmenti sebessége csökken. Ha eléri a térben a
fénysebességet, akkor az időmenti mozgása megszűnik, számára megáll az idő.
(Tudjuk, hogy reális objektum számára ez lehetetlen.) Azt is tudjuk, hogy a
fénysebesség határsebesség, ettől gyorsabban mozogni a térben nem lehet.
(Kivéve a csillagászatban, ahol azt
olvashatjuk, hogy egyes objektumok egymástól való távolodása
fénysebességnél gyorsabban történik.)
Mindezekből egyenesen és szükségszerűen
következik a feltételezés, hogy a térbeli mozgások az időbeli mozgásból
származnak, vagyis a tér az időből "nyílik ki", azaz
a
háromdimenziós világunkat az idődimenzió menti, számunkra láthatatlan FÉNY
hozza létre.
Az idődimenzió mentén
minden egyes pontnak ugyanannyi sebessége, energiája van. Amelyik a térben
egyhelyben áll, az gyorsabban halad, amelyik a térben mozog, az az idő mentén
lassul. Látjuk, hogy a rakéta is 5 egységet használ el az időmenti sebességéből
ahhoz, hogy elérje a B pontot, mert ő a háromszög átlója mentén halad, vagyis
nem csak az időben, hanem a térben is mozog. Ennek következtében viszont
időmenti vesztesége, lemaradása lesz. Vagyis gyakorlatilag egy megmaradási
jelenségről van szó, ami a fizika legáltalánosabb, legalapvetőbb törvénye.
Továbbá azt is látjuk, hogy a térbeli mozgások és az időmenti mozgások között
egyenes, a Pitagorasz-tétellel leírható kapcsolat van. Ahogy nő a térbeli
mozgás, úgy csökken az időmenti mozgás, vagyis a térbeli mozgásnak az időmenti
mozgás szab határt, ami éppen ezért a fénysebességtől nem lehet gyorsabb.
Vagyis ez az ábrázolás választ ad ismert, de ez idáig megmagyarázhatatlan
határkörülményekre is. És így a Pitagorasz-tétel a régi formájában érvényben
marad, így is ki tudjuk számolni a mozgások által okozott térgörbületet, vagyis
a téridőnk, az Univerzumunk újra eukleidészi lesz. Nagyszerű, hiszen a
legutóbbi mérések is egyöntetűen megerősítették, hogy az Univerzumunk nem
hiperbolikus, hanem közel sík, vagyis eukleidészi. A „közel” jelző valószínűleg
az Univerzumban lévő anyagi tömegeknek köszönhető, amelyek a 9. sz. ábra szerit
torzítják a teret, amely mint egy hepehupás hullámfront száguld az idődimenzió
mentén a múltból a jövő felé.
Íme, a helyes téridő
ábrázolás! Viszont felmerülhet a kérdés, hogy mi lehet az, ami az időtengely
mentén a fény sebességével mozog? Mi lenne? FÉNY. Egy olyan fény, amelyet mi
nem láthatunk, amelynek mi csak a térirányú hatásával találkozhatunk. Ez, a
számunkra láthatatlan FÉNY teremti a világot. Ebből a fényből nyílik ki a
tér, miközben a sebessége valamelyest csökken; megjelenik az anyag, megjelenik
a távolság, és a távolsággal az elkülönülés.
Nagyszerű! De még mindig
ott van az a fránya tágulás, amelyet szintén mérések igazolnak. A Világegyetem
egyre tágul, ráadásul a tágulás gyorsul, és a tágulás sebessége arányos az
objektumok egymástól való távolságával. Na, ezt modellezze valaki! Ez a
folyamat egy ilyen szép, közel sík hullámlemezen nem értelmezhető. Sokat
töprengtem, hogyan mozoghatnak azok a teremtő fénysugarak, amelyekből a térbeli
létezésünk keletkezik, mígnem egyszer csak „fény gyúlt” a fejemben: Hát persze,
ha felgyullad egy fényforrás, az minden irányban világít, és nem egy sík
mentén, hanem egy gömbfelület mentén terjed!
Innen már minden egyszerű
lett: A Teremtés pillanatában (ősrobbanás) kiáradó FÉNY egy gömbfelületet, egy
állandóan növekvő gömbfelületet képez. A gömbfelületen ez a FÉNY az energiája
egy részéből kis hullámcsomagokban – kvantumokban – létrehozza a háromdimenziós
világunkat, a teret.

ÍGY JÖN LÉTRE A MI KIS
HÁROMDIMENZIÓS VILÁGUNK! – Hogy miként, az most nem érdekes, viszont a modell
kozmológiai értelemben tökéletes. Tehát miközben a FÉNY folyamatosan terjed, a
gömbfelületen kialakuló Univerzumunk ennek megfelelően folyamatosan tágul. A
tágulás mértéke az objektumok egymástól való távolságától függ.
Leggyorsabban a gömb
ellentétes oldalán lévő objektumok távolodnak egymástól ezek vannak a
legmesszebb egymástól. Minél közelebb vannak ezen a gömbfelületen a pontok
egymáshoz – annál kisebb lesz a távolodás mértéke is. Tehát az Univerzumunk egy
folytonosan táguló fénygömbön helyezkedik el, annak a felületén keletkezik.
Mivel a teremtő FÉNY folyamatosan árad (fénysebességgel), a gömb folyamatosan
növekszik. Azt viszont továbbra sem értjük, hogy az Univerzum miért gyorsulva
tágul. Ennek megfejtését, és azt az ellentmondást és problémát, hogy ez a
gömbfelület miért tűnik számunkra síknak, vagyis eukleidészinek, meghagyom a
fizikusoknak.
4.
A fizikusok nem merik bevallani
Itt tartottam az írásban,
mikor megnéztem Kiss László csillagász Mekkora a
Világegyetem? c YouTube műsorát, melyben Vinkó József csillagásszal
beszélgetnek a témáról. Ebből kiderült számomra, hogy a felfúvódó gömbről –
mint alternatív ábrázolási formáról – már tudnak, de nem értettem, hogy akkor
miért a semmitmondó tölcsérekkel ábrázolják a felfúvódó Világegyetemet? –
Tudniillik az előadásban is ilyen ábrák szerepeltek. Ennek oka csak később lett
világos előttem. Tudniillik 1:13:05-nél nagyon érdekes dolog hangzik el, mikor
a Világegyetem középpontjáról beszélnek:
Vinkó József: „Úgy is
fel lehet ezt fogni, hogy lényegében a 4. dimenzióba tágul bele, van egy 4.
dimenzió, amit mi nem érzékelünk, de lényegében ez a tágulás ez abban történik.
Ezt így is föl lehet fogni…” – és egy nagyot sóhajt, mint aki
megkönnyebbül, hogy végre kimondott valamit, amit egyébként nem lenne szabad.
Kiss László: „Hmmm….
veszélyes megfogalmazások…”
Vinkó: „Igen, igen, ….
nem is akarom én ezt nagyon túltolni …” – és gyorsan témát váltanak.
Vagyis úgy tűnik, hogy a
fizikusok a számításokból már látják a Világegyetem általam leírt alakját, de
az elmélet a tudományos közéletben talán még a „tiltott” kategóriába tartozik,
ezért „veszélyes” dolog ezt hangoztatni.
Nos, kedves Tudós barátaim, helyettetek
én ezt a felismerést – mint egyszerű mérnökember – minden presztízsveszteség
nélkül kijelenthetem. Nem kell félni a 4. dimenziótól, hiszen tudjuk, hogy van,
és azt is tudjuk, hogy nem érzékeljük, és azt is tudjuk, hogy idődimenziónak
hívják. A fent vázolt elmélet szerint a tágulás ebben a láthatatlan dimenzióban
történik, viszont ez azt is jelenti, hogy létezik az éter, vagyis az abszolút
tér, amelyben ez az egész felfúvódás történik, és ez azt jelenti, hogy
Einstein, mikor a relativitáselméletet megfogalmazásakor elvetette az abszolút
tér fogalmát, tévedett.
Az igazságot előbb-utóbb
ki kell mondani, a relativitáselmélet ezen megállapítását meg kell haladni
ahhoz, hogy megértsük a Világmindenség keletkezését. Biztos vagyok benne, ha
Einstein élne, maga is ezt akarná, és meg is tenné, mint ahogy megtette az
általános relativitáselmélet megfogalmazása során elkövetett tévedésével
kapcsolatban is. Nincs tévedhetetlen ember, és az igazságnál a tudomány
világában sincs fontosabb dolog. Különösen akkor, amikor a Teremtő, akiről
tudjuk, hogy Igaz, ilyen revelációszerűen, egyik-napról a másikra, szinte a
semmiből hozza tudomásunkra a Teremtés titkát.
Gyirán István
Kiegészítések:
1. A kérdés tisztázása
során legnagyobb meglepetésemre egy nagyon érdekes anyagot találtam †Dr. Nagy
Sándor neves csillagásztól az Interneten. Ebben a 2003-ban készült, a
tudományos munkában ugyanerről a 4. dimenzióban felfúvódó gömbről beszél,
amiről az írásomban említett fizikusok. A dolgozat névvel és dátummal itt volt
elérhető: http://www.date.hu/~nasa/ati.html
- de időközben eltűnt, viszont név nélkül itt még megtalálható: http://users.atw.hu/rocklive/Text/Mappa2/univerzum1.html
– (Talán csak nem a tudományos külső cenzúra működött? – Mert az öncenzúra léte
nyilvánvaló.)
Tehát a tudósok legalább
20 éve tudnak már a 4. dimenzióban felfúvódó modellről, viszont – amint
hallottuk –, róla beszélni „veszélyes dolog”. Azt viszont nem tudják, hogy a 4.
dimenzió, amelyben a felfúvódás történik, valójában az idődimenzió. Ennek
felismerésére, és a felfúvódás sebességére a Minkowski-tér általam ismertetett
korrigálása vezetett el.
2. Lőrincz Henrik
csillagász, a Természet Világa 2019. júniusi számában megjelent „Értjük-e a
táguló Univerzumot? – Még látom, de már el nem érhetem” című cikkében
ugyanígy mutatja be az Univerzumot:
„A kozmológiai elv
kizárja a kitüntetett középpont létezését, mint ahogy egy felfújódó lufi
kétdimenziós felszínének sincsen középpontja (ebben az analógiában is fontos,
hogy csak a számunkra lényeges részletre koncentráljunk, vagyis csak a lufi
felülete analóg a mi világunkkal, a lufi belseje – és ezzel középpontja – nem
tartozik a modellhez).

2. ábra. Egy táguló
kétdimenziós gömbfelszínen nem található tágulási centrum. Bármely felszíni
megfigyelő saját magát érezheti középpontnak. Egy ilyen zárt Univerzum véges,
de határ nélküli.”
Vagyis a kozmológusok
tudják, hogy az Univerzumunk egy, a 4. dimenzióban lévő gömb felszínén
növekszik, de valamilyen rejtélyes erő miatt ezt nem merik bevallani. Még fel
is hívja a szerző az olvasó figyelmét, hogy a lufi belseje nem tartozik a
modellhez. – Már hogyne tartozna! Hiszen a mérések azt mutatják, hogy
hozzátartozik, mert az Univerzum geometriája így értelmezhető. Ha belátják, hogy
ez a 4. dimenzió valójában az idődimenzió, akkor remélhetőleg megszűnik az
ellenállás, és minden – beleértve Einstein relativitáselméletét is – a helyére
kerül, ami korának felismeréseire kitűnő magyarázatot adott, de az újabb
ismeretek új elméletet követelnek. Viszont Einstein azon sejtése, hogy a fizika
összes törvénye lényegében geometriai tulajdonságokra vezethető vissza,
valószínűleg hamarosan igazolást nyer, ami azt is jelenti, hogy az Univerzumunk
lényegében egy háromdimenziós grafikai történés, vagyis egy látszat. De ez a
felismerés semmit nem vesz el fontosságából, mert elég nagy kiterjedésű ahhoz,
hogy komolyan vegyük, mindössze arról van szó, hogy ezek az újabb felismerések
segítenek felismerni a grafikust, a Teremtőt.